In distributed systems, it is commonly assumed that the network is fully connected, i.e., any two processes are connected through an undirected link. However, there are some studies that consider partially connected networks. In this post, we’ll explore one such study presented in [1].
Model
Consider an asynchronous distributed system composed of the set $\Pi$ of $n$ processes. Assume that up to $f < n/3$ of the processes are Byzantine. A non-Byzantine process is said to be correct. Each process has a unique ID, IDs are not necessarily consecutive, and it is infeasible for a Byzantine process to obtain additional IDs to launch a Sybil attack. Each processes knows $n$, $f$, and the IDs of all processes; accordingly, the system is known (compare this kind of systems with unknown systems [2][3]).
The processes are connected by a communication network represented by an undirected graph $G=(V,E)$ where each node represents a process, and each edge represents a communication link. Each process knows the set of its neighbors. Two processes can directly communicate with each other iff they are neighbors. Otherwise, processes have to rely on others to relay their messages and communicate. Intermediary nodes might be Byzantine, i.e., drop, modify, or inject messages. The communication links are reliable and authenticated. Processes do not have access to digital signatures.
The most interesting result presented in [1]
Theorem. To solve Byzantine reliable broadcast, the communication network must be at least $2f+1$ connected.
Before presenting the proof of the above theorem, we present a preliminary lemma.
Lemma. Consider a distributed system composed of four processes $A, B, C$, and $D$, where $B$ is Byzantine and others are correct. Solving Byzantine reliable broadcast in this system is impossible if processes are connected as follows:
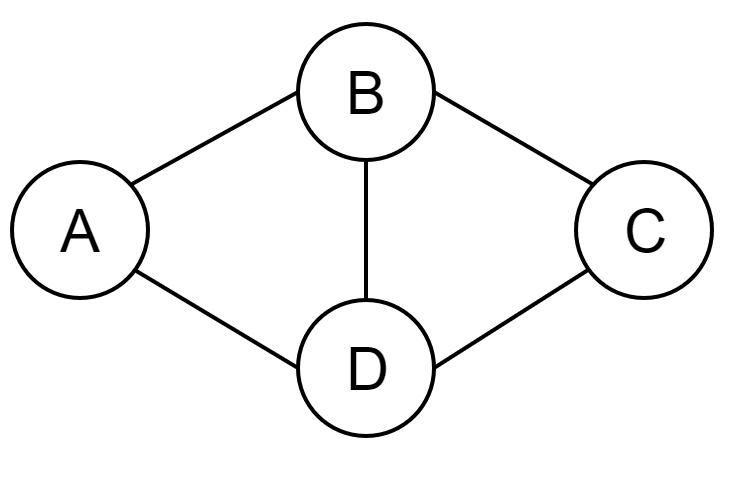
Proof of Lemma. For the sake of contradiction, assume that there is a protocol $\mathcal{P}$ that implements the Byzantine reliable broadcast abstraction even in this system. Recall that one of the properties that $\mathcal{P}$ must satisfy is Validity (i.e., if the sender is correct, then eventually all correct processes will deliver the sender’s message.); besides, it must satisfy No duplication (i.e., every correct process delivers at most one message.) Assume that process $A$ is the sender and broadcasts a message $m$. Consequently, $C$ must deliver $m$. However, assume that $C$ receives two messages: $m$ from $D$ and $m’$ from $B$; now $C$ cannot make a distinction between these messages; hence, it must either deliver both or none of them. If it delivers both messages, No duplication is violated. In case it avoids delivering a message, Validity is violated. Accordingly, $\mathcal{P}$ is not an implementation of the Byzantine reliable broadcast abstraction, which is a contradiction.
We are now ready to present the proof of the above-mentioned theorem.
Proof of Theorem.
Reference
- Unanimity in an unknown and unreliable environment, FOCS, 1981
- On the minimal knowledge required for solving Stellar consensus, ICDCS, 2023
- Knowledge connectivity requirements for solving byzantine consensus with unknown participants, IEEE Transactions on Dependable and Secure Computing, 2016